The Platinum Sequence of Numbers

This analysis uncovers a useful numerical sequence for trading global financial markets, based on a combination of Fibonacci numbers, prime numbers, and Fibonacci ratios.

Starting with the Fibonacci sequence, then incorporating prime numbers, and combining them while maintaining perfect harmony (2.62/6.85).

---

🌀 The Basic Fibonacci Sequence

The Fibonacci sequence is a series of numbers where each number is the sum of the two preceding numbers.

🧮 The sequence's first numbers:

• 0, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987, 1597, 2584, 4181, 6765, 10946, 17711, 28657, 46368, 75025, 121393, 196418, 317811, 514229, 832040, 1346269…

Main Features:

• Each number equals the sum of the previous two (e.g., 3 = 2 + 1 and 5 = 3 + 2).

• Each number is about 1.618 times the preceding number (e.g., 233 ÷ 144 ≈ 1.618).

• Each number is about 0.618 of the next number (e.g., 144 ÷ 233 ≈ 0.618).

Why Are Fibonacci Numbers Important?

Financial markets often form historical highs and lows near Fibonacci numbers. In particular, the 0.618 and 1.618 ratios are among the most important in trading.

⏪ Backtesting on the Dow Jones Industrial (1928–2016)

In my 2018 book Trading World Markets Using Phi and the Fibonacci Numbers, I examined Dow Jones Industrial record highs from October 1928 to April 2016.

As shown in the following table, there were many instances where the DJIA reached a record high close to a Fibonacci number.

Table 1: DJIA Record Highs (1929-2016)

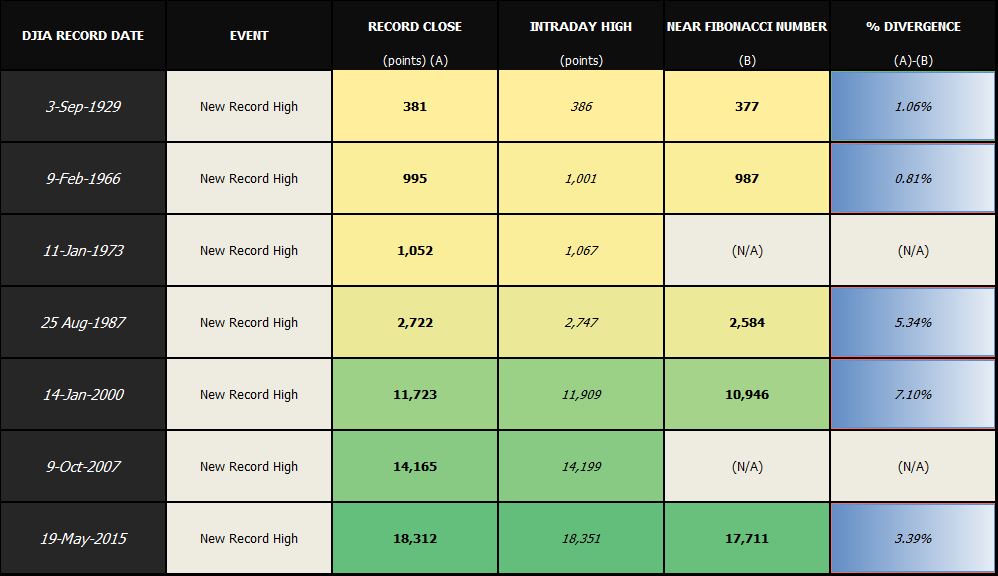
Source: G. Protonotarios (2018)

👉 Results: Out of the seven key historical record highs, in five cases the percentage difference between the record high and the nearest Fibonacci number was less than 7.5%. On the first two occasions (1929 and 1966), the highs almost exactly matched a Fibonacci number (377 and 987). In all cases, the record high was above the corresponding Fibonacci number.

🔗 More: » The book on Amazon

---

⓪ The Prime Numbers

A prime number is a natural number that cannot be formed by multiplying two smaller natural numbers. In other words, a prime number has exactly two factors: 1 and itself.

🧮 List of the first prime numbers:

• 1, 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79, 83, 89, 97….

Characteristics:

• Prime numbers are natural numbers (natural numbers are simply all the positive integers)
• Prime numbers have only 2 factors: 1 and themselves

Why Are Prime Numbers Important?

Prime numbers are important because they are the building blocks of all whole numbers. This analysis will show how to apply them in financial trading.

---

 

🔢 Creating the Platinum Sequence of Numbers (Step-by-Step)

Creating the Platinum Sequence of Numbers in three steps:

Step 1: Selecting the Fibonacci Primes

Starting by selecting numbers that are both Fibonacci numbers and prime numbers. Between 1 and 1 trillion, there are only twelve Fibonacci prime numbers.

Table 2: The first FiboPrimes

---

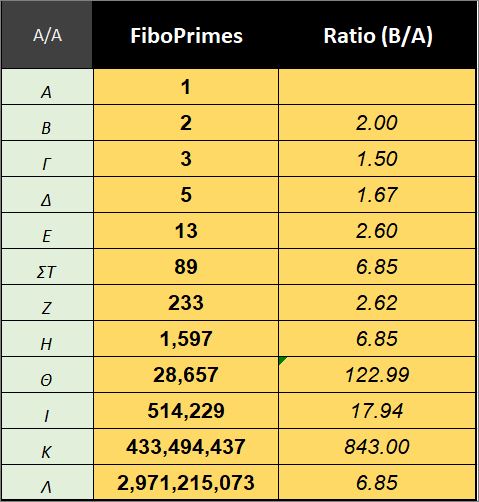
Step 2: Seeking the Missing Harmony (2.62/6.85)

The above sequence of FiboPrimes (Table 2) is interesting, but as a whole, it lacks harmony. Dividing each FiboPrime by the previous one does not produce consistent ratios—the numbers don’t align. Something is missing.

However, up to the number 1,597, we can identify a form of harmony with approximate ratios of 2.62 and 6.85. Why are these ratios important? Because behind 2.62 and 6.85 lies the golden ratio of 1.618.

• 2.618 = 1.618 × 1.618

• 6.854 = 2.618 × 2.618

• 6.854 = 1.618 × 1.618 × 1.618 × 1.618

👉 Note: The golden ratio, or φ, is a fundamental proportion found in mathematics, music, architecture, nature, and even throughout the universe.

---

Step 3: Completing the Platinum Sequence of numbers

The key to uncovering the platinum sequence of numbers is the golden ratio (1.618) and its products, 2.62 and 6.85. To create harmony, we add a few more Fibonacci numbers, seeking order and aiming for perfect harmony.

Table 3: The Platinum Sequence (consisting of only Fibonacci numbers)

👉 Notes:

• All the numbers in the sequence are Fibonacci numbers (but not all Fibonacci numbers are included).
• The sequence includes all Prime numbers that are also Fibonacci numbers.
• The numbers in bold (e.g., 1,597 and 28,657) are the first 12 Fibonacci Primes.
• A few more Fibonacci numbers are added to create perfect harmony (1.618/2.618/6.854).
• The ratio constantly oscillates between 2.618 and 6.854, mimicking the natural vibration of a system. According to the Pythagoreans, this natural vibration is a fundamental property.

---

Final Thoughts

Having used Fibonacci numbers, ratios, and tools for many years, I find them useful in financial trading. The Fibonacci Retracement tool has consistently proven its effectiveness, helping identify key support/resistance levels and price reversals. Furthermore, when an asset’s price breaks historical highs and enters “Price Discovery” territory, Fibonacci Extensions become one of the few reliable tools available to establish potential price targets.

Applying the Platinum Sequence of Numbers in Financial Trading

The Platinum Sequence can be applied when trading any financial market as follows:

• Look for significant price highs and lows near these numbers.

• Watch for potential trend reversals around these numbers.

• If the price crosses a number in the sequence and closes above or below it several times, the next number becomes the theoretical target.

• Apply the sequence not only to prices but also to market caps (price × total number of shares).

Final Verdict

A major change in the fundamental landscape can invalidate any model. Research only matters if you can understand the dynamics of supply and demand, and if you can adapt to what the market is offering at any given time. Remember that no technical analysis model can predict future prices. At best, it can indicate volatility and risk/reward; however, if you know how to use these two elements, that’s all you need.

• The platinum sequence of numbers introduced in this article appears to be a promising addition to Fibonacci numbers and ratios and will be tested in the coming years.

 

■ Trading with Fibonacci Primes -The Platinum Sequence of Numbers

Concept and calculations by Giorgos Protonotarios, Financial Analyst.

for TradingCenter.org (c)

13th of January, 2022